Introduction
This Web Page is intended to serve as an introduction to the GUIPEP software, which is basically PROPEP software (PC version of the Propellant Evaluation Program) with a Graphical User Interface (GUI) added to greatly simplify usage of the program. This highly useful thermochemical software allows the user to evaluate the theoretical performance of a solid (or liquid) rocket propellant. As such, it is particularly useful for checking the viability of possible propellant formulations. As well, it allows the user to quickly determine the most effective ratios of ingredients to achieve desired performance, from a theoretical perspective. GUIPEP is primarily a chemical equilibrium solver, that is, it balances the chemical equations relating the propellant reactants and products by a method known as "minimization of Gibbs free energy". The ingredients (reactants) defining the propellant are transformed adiabatically and irreversibly to reactions product constituents in the amounts fixed by equilibrium relations, chamber pressure, and mass balance at a reaction temperature fixed by the available energy of reaction. The resulting set of products provides the basis for computation of thermodynamic properties from which performance parameters are determined by an iterative process to account for changing product properties and composition. Input is simply a list of propellant ingredients (and the mass of each), as well as chamber pressure and nozzle exit pressure. Solver output includes combustion temperature, isentropic exponent, molecular weight of products, exhaust temperature and composition, specific impulse, and ideal expansion ratio.
Note that burn rate parameters are not evaluated, as burn rate is a complex phenomenon that involves many other physical processes besides combustion, such as heat and mass transfer between the reaction flame and propellant burning surface.
Another similar thermochemical program is CET (Chemical Equilibrium with Transport Properties, NASA TM4557), but as far as I know, no GUI is available for this software. As such, it is cumbersome to use. The predictions are nearly identical to those of GUIPEP, based on my limited experience with using this program.
Analysis Assumptions
The basic assumptions employed by the solver are much as described in the Basic Assumptions Theory Web Page:
- One dimensional flow with regard to the continuity, energy and momentum equations
- Zero flow velocity at the nozzle inlet
- Complete and adiabatic combustion
- Isentropic expansion in the nozzle
- Homogeneous mixing of the reactants and products
- Ideal-gas law applies
- Zero temperature lag and velocity lag of the condensed-phase products
Using GUIPEP
GUIPEP is very easy to use. Up to 10 propellant ingredients are chosen from the drop-down boxes, and the mass (in grams) is entered. Total mass need not add up to 100 grams, but this is the most convenient way to enter the data, as the mass then represents the percentage of that particular constituent.
To eliminate any unwanted ingredient, zero is entered as the mass.
A Title of the run is then entered, and may be up to 10 characters in length.
The Operating Conditions are usually left as the default values, unless there is some particular reason to modify them:
- Temperature of ingredients = 298 K (which is room temperature, 25C.)
- Chamber pressure = 1000 psi (which is the reference pressure at which Isp is quoted).
- Exhaust pressure = 14.7 psi (which is one atmosphere, the condition of ideal expansion at sea level).
As far as Options are concerned, none need be chosen for basic propellant evaluation. However, if the nozzle design is being studied, check the Boost Velocities and Nozzle Design box.
The final step is to run the program by selecting Run, then Single Run. A DOS box then appears to allow execution of the program, which is initiated by hitting the Enter key. MS Notepad then appears, in which the output is displayed.
A screen-shot of an example GUIPEP input screen is shown below:

GUIPEP Output
The initial portion of the output is a basically an echo of the complete input data, as shown below:

Some of the input data is automatically pulled from the pepcoded.daf file, which is a text file that contains the following ingredient data:
- Ingredient name
- Chemical formula
- "Heat of formation" (which is actually delta enthalpy of formation), in calories/gram
- Mass density, in pounds/cubic inch
This data is reflected in the above output, where D-H is the "delta heat of formation", DENS is the constituent density, and COMPOSITION is the chemical formula. Resulting propellant ideal density is also given, and is computed according to the following equation:
 equation 1 equation 1as detailed in the Propellant Grain Theory Web Page.
e.g. DENS = 1/(0.65/0.0767 + 0.34/0.0567 + 0.01/0.184) = 0.06884 lb/in3. The number of gram-atoms of each element present in the ingredients is then listed. Basically, this indicates how many relative atoms of each element are present in the cauldron of ingredients that are combined to form the products of combustion. Although this is key information for the solver, for the user it serves no particular purpose. For reference, this is calculated as the mass to molecular weight ratio for a particular ingredient, multiplied by the mole number for a particular element, summed for each ingredient. The next portion of the output presents the combustion chamber conditions, as shown below:

The first row indicates the combustion temperature (in Kelvin and degrees F), the chamber pressure as specified, the total enthalpy of the mixture (kcal/system mass), total entropy of the system (cal/K/system mass), CP/CV, which is the ratio of specific heats, GAS (number of gas moles in the mixture), and RT/V (a conversion factor which is not normally used). Note that the system mass in this example is 100 grams.
The only important parameters here are:
- Combustion temperature - Also referred to as the Adiabatic Flame Temperature, and determined by the method described in the Combustion Theory Web Page. Generally, the higher the temperature, the higher the specific impulse. Two "real world" factors to consider, however. Higher temperatures require more robust casing and nozzle materials, insulation, or ablative coatings. Note that the chamber temperature is the stagnation temperature that the nozzle will "see" and must be designed for.
Low combustion temperatures, as predicted by this program, may not be self-sustaining in reality. For example, a formulation with a predicted chamber temperature of 1000 K will probably not combust at all.
- CP/CV - The ratio of specific heats, k, for the mixture at combustion chamber conditions, this is correct value to use when calculating characteristic velocity (cee-star) and chamber pressure, as described in the preceding Theory Web Pages. The value of CP/CV is calculated from the following equations:
 where where  equations 2 & 3 equations 2 & 3
with the details on notation and use of the equations provided in the
Technical Notepad Web Page.
- GAS - The number of moles of gaseous combustion products in the product mixture (which may also contain condensed phase). This value is used to calculate the effective Molecular Weight, M, of the product mixture, which is given by dividing the number of gas moles into the system mass. For this example, M = 100/ 2.297 = 43.54 g/mole. This is the proper molecular weight value to use in the gas dynamics equations described in the preceding Theory Web Pages.
The next two lines provide the values of the molar specific heat of the gaseous products and of the mixture, (cal/mole/K), and are provided for reference only.
The following line provides the values for the number of gas moles (repeated) and the number of moles of condensed phase products, which may be solid or liquid. This information is of interest, as it provides the (molar) ratio of gas/condensed phase products.
The next lines of output tabulate the number of moles of each combustion product constituent. Product names followed by * are liquid phase, and & designates solid phase; all others are gas phase. This data allows the user to calculate the mass fraction of condensed phase, which is given by the mass of all condensed phase divided by the system mass, and where the mass of any constituent is given by the number of moles multiplied by the molecular weight of that constituent.
e.g. Mass fraction of condensed phase = [(0.30541) 138.2 + 0.01242 (71.9)]/ 100 = 0.422 Many of the combustion products are in trace amounts, and play a negligible role in the overall process. From the example above, the only significant products are H2O, K2CO3, CO2, H2, CO, N2 and perhaps KOH and FeO.
For best performance, low molecular weight products are desirable, such that the effective molecular weight of the mixture is minimized. Low molecular weight products in the above example would be H2O, H, H2, CH4, CO, NH3 and OH. The next line in the above portion of the output gives the molecular weight of the mixture (sometimes denoted MW), which is given by the sum of the mole fraction, for each constituent, multiplied by its molecular weight, as shown below:
 equation 4
This value of molecular weight should be neglected as it serves no purpose with regard to rocket performance. equation 4
This value of molecular weight should be neglected as it serves no purpose with regard to rocket performance.
The next portion of the output presents the nozzle exhaust conditions, as shown below:

The format of these results is identical to that of the chamber results. The values represent the conditions at the exit plane of the nozzle. 
Some points worth noting:
- The combustion product temperature has dropped significantly, as thermal energy has been converted to kinetic energy. The exit temperature may be calculated from equation 4 of the Nozzle Theory Web Page.
: where where  equations 5 & 6 equations 5 & 6
where To is the chamber temperature, Po/Pe is the chamber/exit pressure ratio, Me is the mach number of the flow at the exit, and k is the CP/CV for exhaust conditions. Note that the value given in the output is for conditions of shifting equilibrium which is explained later.
- Chamber pressure has dropped to one atmosphere, the design condition.
- Both CP/CV and the number of gas moles has changed slightly, reflecting the changing composition and temperature of the exhaust as it flows through the nozzle.
- Likewise, the specific heats and number of moles of condensed species has changed from chamber conditions.
- The composition of the products has changed in an interesting way. Note that there are fewer trace constituents. This is because the temperature is lower and less dissociation (breaking up into simpler molecules) of the larger compounds occurs. Also note that the liquid products have frozen into solid phase.
The next portion of the output presents the Performance of a rocket motor equipped with this propellant and nozzle as specified:

Performance is given for both Frozen and Shifting equilibrium conditions.
What do these terms mean? Frozen equilibrium means that the chemical composition of the exhaust does not change as it flows through the nozzle (product composition is established in the combustion chamber). Shifting equilibrium assumes that instantaneous chemical equilibrium is established as the gas expands through the nozzle, "shifting" the composition continuously.
Why are both results provided? Because of the very short residence time in the nozzle, it is uncertain whether or not there is sufficient time for chemical reactions to actually occur as predicted by the shifting equilibrium model. Geometry also plays a role, as longer nozzles provide more residence time.
Which results to use? For amateur motors, where nozzles are very small in comparison with large professional rockets, I consider the frozen flow model to be more realistic. For the Kappa rocket motor nozzle, I've calculated the time duration for the flow to pass through the nozzle to be 430 microseconds!
In the performance portion of the output, the first row presents the ideal Specific Impulse (IMPULSE), isentropic exponent (IS EX), flow temperature at the throat (T*) and pressure at the throat (P*), characteristic velocity (C*), vacuum impulse (ISP*), optimum expansion ratio (OPT-EX), density Isp (D-ISP), throat area-to-mass flow rate (A*M), and exit-plane temperature (EX-T).
The following is a brief discussion of each of the results:
- Ideal Specific Impulse is the key "yardstick" of performance potential, and can be considered to relate the thrust produced by a unit mass (e.g. 1 lb or kg) of propellant over a burning time of one second. The ideal Specific Impulse may be determined from equation 7 of the Impulse and C* Theory Web Page:
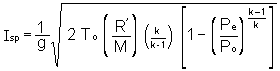 equation 7 equation 7where k is taken as the average of CP/CV for chamber and exhaust conditions, and M as the average effective molecular weight for chamber and exhaust conditions.
- The isentropic exponent is the same as k or CP/CV for a perfect gas such that PVk = constant (P=pressure; V=volume). As the gas is not perfect, the values of IS EX and CP/CV do not agree.
- T* and P* are the so-called critical values of the flow temperature and pressure where the flow velocity is mach one, that is, at the throat. These may be calculated from equations 4 & 6 of the Nozzle Theory Web Page. Units are Kelvin and atmospheres, respectively.
 and and  equations 8 & 9 equations 8 & 9
- C* is the Characteristic Exhaust Velocity (cee-star), with units of feet/sec. This parameter may be considered to be a figure of thermochemical merit for a particular propellant, and is given by equation 3 of the Impulse and C* Theory Web Page:
 equation 10 equation 10
- ISP* is the vacuum impulse that would be obtained by a sonic nozzle in air-breathing motor work, and thus may be ignored.
- OPT-EX, the Optimum Expansion Ratio (Ae/At) is an important parameter in nozzle design. This value defines the ratio of the nozzle exit area to throat area, and as such, sizes the divergence cone exit diameter, where
 . This ratio may be determined from equation 14 of the Nozzle Theory Web Page: . This ratio may be determined from equation 14 of the Nozzle Theory Web Page: equation 11 equation 11
where k is the value of CP/CV for exhaust conditions.
- The Density Specific Impulse, D-ISP, is an interesting parameter. It is defined as the product of specific impulse and the propellant specific gravity, or Id = Isp dp (the specific gravity is numerically equal to the density, in gram/cc). A high value of Density Isp would be important for compact motor designs, where volume is at a premium.
- A*M ("A-star M") is the ratio of nozzle throat area to mass flow rate expressed as in2-sec/lb. I really don't know what this is meant to be used for...!
- EX-T is the nozzle exit plane temperature (Kelvin) and may be determined from equation 5 shown earlier.
Comparison of Performance Equations to GUIPEP
The following table shows an interesting comparison between the results presented by GUIPEP to the same results as calculated by use of the performance equations presented above, which are considered to be "approximate". Nevertheless, the results are in very close agreement.

Limitations of GUIPEP
To some extent, the accuracy of the results is dependant upon the JANNAF.DAT file which contains reaction species heat of formation data used by the solver. The species list is limited in scope, and for unusual propellant combinations, the actual reaction products may not be present in the list. The result is a failure of the solver, or inaccurate results. A good example is Zinc-Sulphur propellant, for which GUIPEP does not provide any solution. The reason is that the main product of combustion, zinc sulphide, is not present in the list of reaction species.
As mentioned in the introduction, propellant burn rate is not assessed by GUIPEP, nor is there any indication provided as to whether a particular propellant concoction will be self-combusting. Although it is obvious that this sort of assessment is beyond the scope or intent of GUIPEP, this fact must be kept in mind when evaluating a propellant. A good example is ammonium nitrate (AN) based propellants. Although GUIPEP typically presents glowing numbers for performance, in reality, the burn rate is usually so slow that the propellant will self-extinguish. Also, the addition of metals such as aluminum is found to boost performance significantly for many propellants, according to GUIPEP results. This is usually not the case in reality, where much of the metal is left unburned unless the propellant reaction temperature is very high and the metal particle size is very fine. Physical limitations also may negate a potentially promising propellant. High solids loading is often predicted to improve performance, but in practice, is usually difficult to achieve due to binder adhesion limitations.
Another limitation, or shortcoming, relates to the prediction of performance of propellants with significant percentage of condensed phase particles in the exhaust (two-phase flow). The value of CP/CV and the isentropic exponent used by the GUIPEP solver for determination of all the performance parameters are calculated for a gas-particle mixture, as shown in Equation 1 of the Two-phase Flow Theory Web Page. However, for flow through the nozzle, a modified isentropic exponent should be used, as given by Equation 2 in the referenced web page. For propellants with minimal condensed-phase fraction (say, <10%), the overall effect is probably negligible. But for a propellant such as KN-Sucrose, where the condensed-phase fraction is very high (44%), the net effect is more significant. As an example, the chamber value of the isentropic exponent as calculated by Equation 2 is k=1.04, whereas the value given by Equation 1 and GUIPEP is k= 1.13. The difference in Ideal Specific Impulse is Isp= 166 sec. versus Isp= 153 sec., respectively.
|


 equation 1
equation 1 equation 4
equation 4