

Nozzle Theory
The rocket nozzle can surely be described as the epitome of elegant simplicity. The primary function of a nozzle is to channel and accelerate the combustion products produced by the burning propellant in such as way as to maximize the velocity of the exhaust at the exit, to supersonic velocity. The familiar rocket nozzle, also known as a convergent-divergent, or deLaval nozzle, accomplishes this remarkable feat by simple geometry. In other words, it does this by varying the cross-sectional area (or diameter) in an exacting form.
Fluid properties, such as velocity, density, pressure and temperature, in compressible fluid flow, are affected by
Typical nozzle cross-sectional areas of particular interest are shown in the figure below  The analysis of compressible fluid flow involves four equations of particular interest:
The energy equation is a statement of the principle of conservation of energy. For adiabatic flow between any two points, x1 and x2 , it is given by 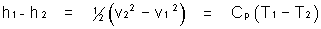  where h represents enthalpy of the fluid (which can be considered the energy available for heat transfer), v is the flow velocity in the x-direction, Cp is the effective heat capacity of the fluid, and T is the fluid temperature. It is apparent, then, that the properties of a fluid (e.g. temperature) are a function of the flow velocity. In describing the state of a fluid at any point along its flow, it is convenient to consider the stagnation state as a reference state. The stagnation properties may be considered as the properties that would result if the fluid were (isentropically) decelerated to zero velocity (i.e. stagnant flow). The stagnation temperature, To, is found from the energy equation (by setting v2=0) to be  equation 1 equation 1For an isentropic flow process, the following important relationship between stagnation properties for Temperature, Pressure, and Fluid Density hold  equation 2 equation 2where k is the all-important ratio of specific heats, also referred to as the isentropic exponent, defined as 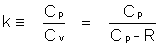 Both Cp and R (specific gas constant) are properties determined by the composition of the combustion products, where R = R'/ M, where R' is the universal gas constant, and M is the effective molecular weight of the combustion products. If the combustion products contain an appreciable percentage of condensed phase particles (smoke), the value of the effective molecular weight, M, must account for this. As well, the proper k must be used which takes into account two-phase flow. The determination of k and M for the combustion products is detailed in the Technical Notepad #1 Web Page.
The local sonic velocity, a, and the Mach number, M, (defined as the ratio of the flow velocity to the local sonic velocity), is given by  equation 3 equation 3From equations 1,2 & 3, the relationship between the stagnation temperature (also referred to as total temperature) and Mach number may be written as  equation 4 equation 4It can be shown from the first and second laws of thermodynamics, for any isentropic process, that  equation 5 equation 5From equations 4 & 5, and from the equation of state for an ideal gas,  , the relationship between stagnation pressure; density and Mach number may be expressed as given in the following two equations , the relationship between stagnation pressure; density and Mach number may be expressed as given in the following two equations
 equation 6 equation 6 equation 7 equation 7
Equations 4, 6 & 7 are particularly useful, as these allow each property to be determined in a flow if the Mach number and the stagnation properties are known. The stagnation (or total) properties To, Po, and Another important stagnation property is the stagnation enthalpy. This is obtained from the energy equation (by setting v2=0)  equation 8 equation 8Physically, the stagnation enthalpy is the enthalpy that would be reached if the flow (at some point) were somehow decelerated to zero velocity. It is useful to note that the stagnation enthalpy is constant throughout the flow in the nozzle. This is also true of the other stagnation properties (temperature, pressure, and density). The second of the four equations of interest regarding compressible fluid flow, as discussed earlier, is the continuity (or conservation of mass) equation, which is given by 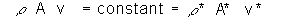 equation 9 equation 9where A is the nozzle cross-sectional area, v is the velocity of the flow. This equation simply states that the mass flowing through the nozzle must be constant. The "star" (asterisk) signifies a so-called critical condition, where Mach number is unity, M=1 (flow velocity is equal to the speed of sound). The importance of the critical condition will soon be made apparent. Taking equations 3, 4, 7 & 9, it is possible to express the area ratio, A/A*, in terms of the Mach number of the flow. The area ratio is simply the cross-sectional area at any point (x) in the nozzle, to the cross-sectional area where the critical condition exists (M=1)
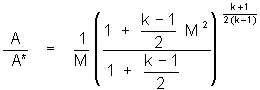 equation 10 equation 10
Since the Mach number can be determined by knowing the area ratio, it is now possible to plot the variation of the temperature, pressure and fluid density throughout the nozzle, by use of equations 4, 6 & 7. A plot of these properties is given in Appendix C, for the Kappa nozzle. From equations 8 & 9, the flow velocity at the nozzle exit can be expressed as  equation 11 equation 11where subscripts e and x signify exit and any point x along the nozzle axis, respectively. This equation can then be put into the far more useful form with the aid of the energy equation and the definition of k, as well as equation 2.
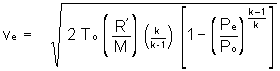 equation 12 equation 12This equation is one of the most useful, as it allows the nozzle exit velocity to be calculated. In summarizing, it is necessary to know
A better understanding of the nozzle behaviour may be obtained by looking closely that this equation. It may be seen that
The ratio between the throat area, A*, and any downstream area in the nozzle, Ax, at which pressure Px prevails can be conveniently expressed as a function of the pressure ratio, Px /Po, and k. By noting that at the throat M is unity, and using equations 2, 3, 4, 7 & 12, leads to  equation 13 equation 13
This is another important and useful equation. It allows the exit area, Ae, to be calculated such that the exit pressure, Pe, is equal to the ambient pressure, Pa (typically 1 atm.), by simply substituting Pa for Px.
This is known as the nozzle design condition. For such a condition maximum thrust is achieved (derivation). For this design, the area ratio Ae /A* is known as the all-important Optimum Expansion Ratio.
For a highly informative explanation on convergent-divergent nozzle operation, in particular choked flow and shock formation, visit the
Nozzle Applet website (includes a simulation).
Example #1 - Calculate nozzle area ratio (A/A*) with varying Mach number and plot on a graph
Example #2 - Calculate flow properties Temperature, Pressure and Density with varying Mach number and plot on a graph
Example #3 - Calculate nozzle Optimum Expansion ratio for a rocket motor operating at 65 atmospheres chamber pressure expanding to ambient air.
Example #4 - Calculate nozzle flow exit velocity for a rocket motor operating at 68 atmospheres chamber pressure, expanding to ambient air, using KNSB as propellant. |
