| C12H22O11 | -2222.1 |
| KNO3 | -494.63 |
| CO2 | -393.52 |
| CO | -110.53 |
| H2O | -241.83 |
| H2 | 0 |
| N2 | 0 |
| K2CO3 | -1150.18 |
| KOH | -424.72 |
Using the energy balance equation (assuming no changes in K.E. or P.E.):
Substituting in the values for hf , ni and ne gives :
1 (-2222.10 + 0) + 6.288(-494.63 + 0) = 3.796(-393.52 + 
CO2) + 5.205(-110.53 + CO) + 7.794(-241.83 + H2O) + 3.065(0 + H2) + 3.143 (0 + N2) + 2.998 (-1150.18 + K2CO3) + 0.274 (-424.72 + KOH)
Expanding and gathering terms simplifies the equation to the following form:
2186.2 = 3.796CO2 + 5.205 CO + 7.794 H2O + 3.065 H2 + 3.143 N2 + 2.998 K2CO3 + 0.274 KOH
Solution of the equation is obtained by simply substituting in values for at a certain temperature. This temperature is equal to the AFT when the the right hand side of the equation is equal to the left hand side (=2186.2).
Take a guess that the AFT lies somewhere between 1700 K and 1800 K (easy for me to guess, as I know the answer! But no matter what the guess, the answer will eventually converge).
From the JANAF tables, the values of are: (units are kJ/mole)
| T | CO2 | CO | H2O | H2 | N2 | K2CO3 | KOH |
| 1700 K | 73.480 | 45.945 | 57.758 | 42.835 | 45.429 | 280.275 | 116.505 |
| 1800 K | 79.431 | 49.526 | 62.693 | 46.169 | 48.978 | 301.195 | 124.815 |
For the term on the right side of the equation, substituting in the values at T=1700K :
3.796 (73.480) + 5.205 (45.945) + 7.905 (57.758) + 3.065 (42.835) + 3.143 (45.429) + 2.998 (280.275) + 0.274 (116.505) = 2114.5 kJ/mole
Substituting in the values at T=1800 K:
3.796 (79.431) + 5.205 (49.526) + 7.794 (62.693) + 3.065 (46.169) + 3.143 (48.978) + 2.998 (301.195) + 0.274 (124.815) = 2280.6 kJ/mole
Clearly, the actual temperature lies in between 1700 and 1800 K. The actual value may be found by using linear interpolation:
This is in close agreement with the combustion temperature predicted by GUIPEP (1720 K.), that being about 1% lower. The small deviation is a result of the simplified combustion equation assumed in this example. In reality, some trace products such as NH3 and monatomic K form, consuming energy in the process.
Appendix B
Reserved for future use.
Appendix C
The following are plots of the nozzle flow properties for the Kappa-DX rocket motor:
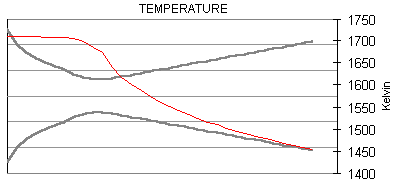
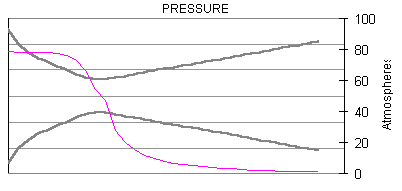
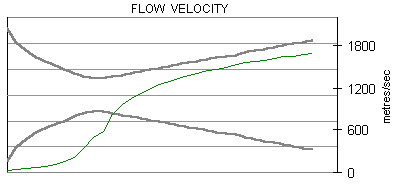
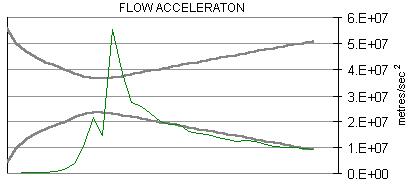
Time for flow to travel through nozzle = 430 microseconds.
Appendix D
The derivation of the expression for mass flow rate through the nozzle is presented here.From Equation 9 of the Nozzle Theory Web Page, the continuity equation for mass flow rate through the nozzle is given by:
where * designates critical (throat) conditions. From Equation 7 of the referenced web page, the critical flow density may be written as:
and from Equations 3 & 4, the critical (sonic) velocity may be given by:
From the ideal gas law, the chamber density may be expressed as:
Substitutionof this equation and those for critical density and velocity into the mass flow rate expression gives:
which may be rearranged to the form of the expression shown as Equation 4 of the Chamber Pressure Theory Web Page:
Units of measure:
Equation 12 of the Chamber Pressure Theory Web Page:
Therefore,Appendix E
Example: Calculate the maximum steady-state chamber pressure for the design of the Kappa-DX rocket motor.
The most prudent (botch-proof) system of units is mks (metre : kilogram : second), however, for this example, appropriate English units will used, as well.
Burn/throat area Kn, max. = 378 Propellant density 
p = 1.806 g/cm3 = 1806 kg/m3 = 0.00203 slug/in3Burn rate r = 12.65 mm/s = 0.01265 m/s = 0.50 in/s Propellant c-star c* = 912 m/s = 2992 ft/s
Po = 378 (1806) .01265 (926) = 7.9 x 106 N/m2 ( 7.9 MPa)
or
Po = 378 (0.00203) 0.50 (2992) = 1148 psi
