Richard
Nakkas Experimental Rocketry Web Site

Solid Rocket Motor
Theory Two-phase Flow
Example 2
Utilizing KNSU
propellant, calculate the ideal chamber pressure, thrust and thrust coefficient
for the following rocket motor conditions with optimum nozzle expansion:
· Kn = 250
·
Throat diameter 12.0 mm
(0.472 inch):
Equation 15 presents Chamber Pressure for two-phase mixture:
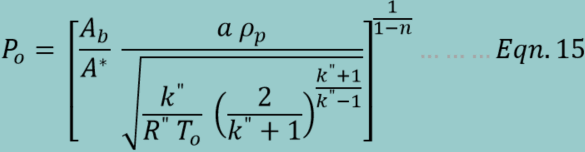
The values for kʺ,
Rʺ and To are obtained
from Example 1:
kʺ = 1.133
Rʺ = 197.9 J/kg-K
To = 1720 K.
The burn rate parameters and propellant
density are taken from KNSU Propellant Chemistry and Performance Characteristics web page:
burn rate coefficent a = 0.0665 inch/sec/psin
pressure exponent n = 0.319
We are using the mks
(metres/kilogram/second) system of units, so the value of a
must be converted:
![]() m/sec/Pan
m/sec/Pan
note: Pa is Pascal = N/m2
The pressure
exponent, n, is dimensionless so no conversion is
required.
ρp = 1.89 g/cm3
= 1890 kg/m3
Ab/A* =
Kn = 250
These values are
plugged into Equation 15 to obtain ideal chamber pressure:

(rounded
to 4 signficant figures)
Note 6520000 Pa = 6.52 MPa = 946
psi
Motor thrust for
two-phase condition is given by Equation 13:

The
cross-sectional area of the nozzle throat is calculated from the diameter:
A*
= Ό π (0.012)2 = 0.000113 m2
The chamber
pressure was calculated to be 6.52 MPa. Optimum expansion requires the pressure
at the nozzle exit to be atmospheric, or Pe = 101.3 kPa.
This gives the expansion ratio:
Pe/Po
= 101300/6520000 = 0.0155
Plugging these
values into the equations to solve for thrust gives:
 1202
N.
1202
N.
The
thrust coefficient, Cf,
is given by Equation 14. As the thrust coefficient is simply the amplification
factor by which the thrust is increased relative the the thrust that is
obtained by the chamber pressure, Po, acting over
the throat area, A*, the Cf
is simply the terms on the right-hand side of Equation 13.
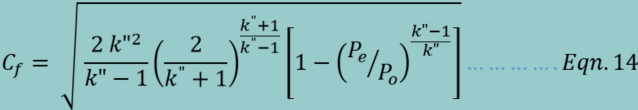

The
thrust is therefore amplified by 63.3% as a result of flow expansion in the divergent
portion of the nozzle.
Originally
posted March 3, 2023
Last updated March 22, 2023