Richard
Nakkas Experimental Rocketry Web Site

Solid Rocket Motor
Theory Two-phase Flow
Example 1
For
KNSU propellant, calculate the various two-phase thermochemical and performance
parameters:
·
Molecular mass, specific
gas constant and ratio of specific heats
·
Critical (throat)
velocity, Characteristic Exhaust Velocity
·
Exhaust velocity and
Specific Impulse (ideal expansion from 1000 psi chamber pressure)
The
first step is to run ProPep to obtain the products of combustion:
Code WEIGHT D-H
DENS COMPOSITION
0 POTASSIUM NITRATE 65.000 -1169
0.07620 1 N 3 O
1 K
0 SUCROSE (TABLE SUGAR) 35.000 -1550
0.05740 22 H 12 C
11 O
THE
PROPELLANT DENSITY IS 0.06836 LB/CU-IN
OR 1.8923 GM/CC
THE
TOTAL PROPELLANT WEIGHT IS 100.0000
GRAMS
NUMBER
OF GRAM ATOMS OF EACH ELEMENT PRESENT IN INGREDIENTS
2.249436 H
1.226965 C
0.642877 N
3.053349 O
0.642877 K
****************************CHAMBER
RESULTS FOLLOW
*****************************
T(K)
T(F) P(ATM) P(PSI) ENTHALPY ENTROPY
CP/CV GAS RT/V
1720
2636 68.02 1000.00
-130.24 165.92 1.1331
2.382 28.559
SPECIFIC
HEAT (MOLAR) OF GAS AND TOTAL =
10.505 14.984
NUMBER
MOLS GAS AND CONDENSED = 2.382 0.307
7.969284e-001 H2O 5.322495e-001 CO 3.880990e-001 CO2 3.213577e-001 N2
3.134432e-001 H2 3.065426e-001 K2CO3* 2.796753e-002 KHO 1.473071e-003 K
1.537422e-004 K2H2O2 1.005049e-004 NH3 1.856416e-005 H 1.306551e-005 KH
1.042846e-005 KCN 6.919009e-006 CH4 3.484479e-006 CH2O 3.326461e-006 CNH
2.62602E-06 HO
The
next step is to calculate the number of moles, mole fraction, mass and mass fraction
for each of the major products of combustion. Trace products such as K, K2H2O2, NH3 will be
neglected. The products are separated in terms of condensed phase and gaseous.
For KNSU, the sole condensed phase product is potassium carbonate (K2CO3).
ProPep indicates liquid products with an asterisk (*) and solids with an
ampersand (&). The calculations are most conveniently done using a
spreadsheet app such as Excel. The
results for KNSU are shown in Table 1.

Table 1
The
molecular mass (MW) for the products may be found at Wikipedia
or NIST Chemical Webbook.
Using
nitrogen, gas N2, as an example, the mole
fraction, mass and mass fraction are calculated as such:
· mole fraction N2 = # moles N2 / # moles gas = 0.3214/2.380 = 0.1350
· mass N2 = MW N2
Χ # moles N2 = 28.02 Χ0.3214 = 9.004 grams
· N2 mass fraction of gases =
mass N2/mass gas = 9.004 / 57.556 = 0.1560
· N2 mass fraction of mixture= mass N2/mass
mixture = 9.004 / 100.0 = 0.0900
The mass fraction of condensed phase, X,
is calculated as:
X = mass condensed /
total mass of products = 42.367 / 100 = 0.424
Effective molecular mass, Mʺ, is
calculated as:
Mʺ = total product
mass / number of gas moles = 100.0 / 2.38 = 42.02 grams/mole
Specific
gas constant, Rʺ, is calculated as the
universal gas constant divided by the effective molecular mass: (where ![]() = 8314 J/kmol-K)
= 8314 J/kmol-K)
Rʺ = ![]() / 42.02 = 197.9 J/kg-K
/ 42.02 = 197.9 J/kg-K
The
specific heat of the condensed phase products, Cs,
and the gaseous products, Cp, is found
using Eqn.4a:
![]()
Both
Cs and Cp are
functions of temperature. As such, we will determine the values of the specific
heat of the products at chamber conditions (To) and assume
a frozen-flow model whereby the products of combustion do not change as the
products flow through the nozzle. Alternatively, the average temperature of the
products from chamber conditions to nozzle exit conditions can be used,
however, the simplification of using chamber temperature results in a small
overall difference.
The
specific heat for each of the products at the combustion temperature is
calculated using the Shomate polynomial equation:
Cp = A + B*t + C*t2 + D*t3 + E/t2
where Cp
= heat capacity (J/mol*K) and t = temperature (K) / 1000. The values for the
polynomial coefficients can be found at the
NIST Chemical Webbook.
Using nitrogen gas (N2) at KNSU combustion temperature of 1720 K. as an example:
Valid for temperature range 500K
2000K
A 19.50583
B 19.88705
C -8.598535
D 1.369784
E 0.527601
This gives, for N2
at 1720 K:
![]() 35.42 J/mol-K
35.42 J/mol-K
Once
again, using Excel greatly eases the
calculations and minimizes potential for calculation error. The results for all
the KNSU products are shown in Table 2.

Table 2
Note that the units applicable to the Shomate equation are Joules per mole-Kelvin (J/mol-K). We want the heat capacity
to be per unit mass. In the second row in Table 2, the units of J/gram-K are arrived at by dividing the molar Cp by the molecular mass of each product. The Cp for the gas-only mixture and the Cp for
the gas-condensed mixture is given by Eqn.4a:
![]()
Note that mi/mp
(i=1,2,3
) is the mass fraction
of the particular product as calculated in Table 1. This results in the
following:
![]()
![]()
The unit of measure we need to use for the thermochemical
calculations is Joules per kilogram-Kelvin (J/kg-K) and as such, the values we
need for Cp(gas), Cpmix and
Cs are each multiplied by 1000, giving:
Cp (gas) = 1813.4 J/kg-K
Cpmix = 1685.0 J/kg-K
Cs = 1513.6 J/kg-K
The specific heat ratio for the mixture is calculated using Eqn.3
![]()
Giving
![]()
The isentropic exponent for two-phase flow, kʺ, obtained from gasdynamics analysis, is given by either Eqn.5a or 5b. Using equation 5b:
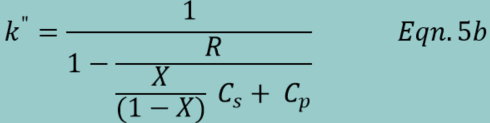

As expected, this is identical to the value for the mixture.
The
critical (throat) velocity for KNSU is calculated using Eqn.6b

Plugging
in the values for kʺ, Rʺ
and To gives:

Characteristic Exhaust Velocity, or c-star,
is given by Equation 7:

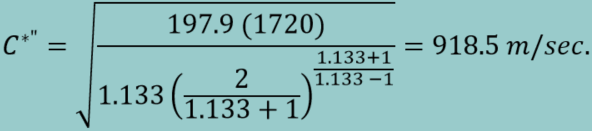
The
nozzle exhaust velocity is given by Equation 8:

Giving the exhaust velocity for KNSU
at 1000 psi with optimum expansion (Pe/Po = 0.0147):
![]()
![]()
The specific impulse is given by
Equation 10:
![]()
So for KNSU, the ideal specific impulse is:
![]()
Originally
posted March 1, 2023
Last updated March 22, 2023