Introduction
The burning surface of a rocket propellant grain recedes in a direction perpendicular to this burning surface. The rate of regression, typically measured in inches per second (or mm per second), is termed burning rate (or burn rate). This rate can differ significantly for different propellants, or for one particular propellant, depending on various operating conditions as well as formulation. Knowing quantitatively the burning rate of a propellant, and how it changes under various conditions, is of fundamental importance in the successful design of a solid rocket motor. This web page discusses the factors that influence burn rate, how it may be modified, how the burn rate can be determined experimentally, and the physical processes that occur at the burning surface of a propellant that governs the burning rate.What Influences Burning Rate?
An illustration of the concept of burning surface regression is given in Figure 1, for a section of a hollow cylindrical grain, with an inhibited outer surface ( "inhibited" means that the propellant surface is protected from the heat of combustion and as such, burning does not occur). Burning commences along the length of the central core, with the burning surface receding radially outward (shown at arbitrary times t1, t2, t3). Note that the burning surface area (represented by the arc length of the red lines in this figure) is continually increasing. Also note that the surface regression rate (burn rate) is not constant. These two events are, in fact, directly related, as will be discussed shortly.

Propellant burning rate is influenced by certain factors, the most significant being:
- Combustion chamber pressure
- Initial temperature of the propellant grain
- Velocity of the combustion gases flowing parallel to the burning surface
- Local static pressure
- Motor acceleration and spin
- Burn rate is profoundly affected by chamber pressure. For example, KNSU has a burning rate of 3.8 mm/sec. at 1 atmosphere. However, at 68 atmospheres (1000 psi), the burn rate is about 15 mm/sec., a four-fold increase. The usual representation of the pressure dependance on burn rate is the Saint Robert's Law (a.k.a. Vieille's Law):
r = ro + a Pc n where r is the burn rate, ro is a constant (usually taken as zero), a is the burn rate coefficient, and n is the pressure exponent. The values of a and n are determined empirically for a particular propellant formulation, and cannot be theoretically predicted. Various means may be employed to determine these parameters, such as a Strand Burner or Ballistic Evaluation Motor (BEM). It is important to realize that a single set of a, n values are typically valid over a distinct pressure range. More than one set may be necessary to accurately represent the full pressure regime of interest, as illustrated in Figure 2.
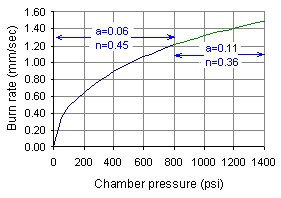
Figure 2 -- Saint Robert's model of burn rate v.s. pressure (example)
When plotted on log-log scales, the Saint Robert's function is a straight line.
Certain propellants (or with additives) deviate from this behaviour, and exhibit sharp changes in burn rate behaviour. These type of propellants are termed plateau or mesa propellants, as illustrated in Figure 3. Both the KNDX and KNSB propellants exhibit this behaviour, the former plateau, and the latter, mesa (see KNDX & KNSB Propellants -- Burn Rate Experimentation). Plateau and mesa effects may be the result of different rates of surface regression (as a function of pressure) of the binder compared to the oxidizer particles. Another explanation is that the condensed phase combustion products may "pool" and retard heat transfer to the surface at elevated pressure levels.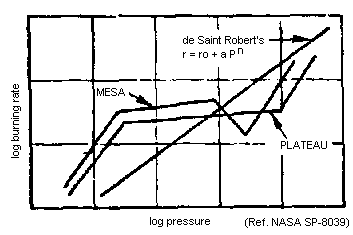
Figure 3 -- Plateau and mesa behaviour
Burning rate can be particularly sensitive to the value of the pressure exponent, n (the slope of the log-log curve in Fig.3). High values of n can produce large changes in burning rate with relatively small changes in chamber pressure, with potentially catastrophic consequences, as higher burning rate leads to even greater chamber pressure. Another reason why a high pressure exponent may be undesireable (at least for amateur motors) is due to the low sensitivity of burn rate, due to pressure, at the low end of the pressure regime. This can result in difficult starting, with the motor simply refusing to "come up to pressure". This low sensitivity to pressure, for high pressure exponents, becomes more clear if we consider a pressure exponent of unity (n=1). This implies burn rate beinging directly, or linearly, proportional to chamber pressure. The slope of the burn rate v.s. pressure curve is a straight line. Figure 4 illustrates the pressure profile for various values of n. It can be seen that with a low value of pressure exponent, for example n=0.2, the burn rate changes very rapidly at low pressure, providing excellent motor start-up capability.
Figure 4 -- Effect of various pressure exponents on burning rate sensitivity to pressure
If the value of the exponent is close to zero, the burning rate is largely insensitive to pressure, and unstable combustion may result. For these reasons, the pressure exponent for a practical propellant should have a value between 0.3 and 0.6 in the regime of the motor steady-state operating condition. - Temperature affects the rate of chemical reactions and thus the initial temperature of the propellant grain influences burning rate. If a particular propellant shows significant sensitivity to initial grain temperature, operation at temperature extremes will affect the time-thrust profile of the motor. This is a factor to consider for winter launches, for example, when the grain temperature may be 20 or more degrees (C.) lower than "normal" launch conditions. Both the KNDX & KNSB Propellants seem to show minor sensitivity to temperature over the range of 0oC to 40oC. (see KNDX & KNSB Propellants -- Burn Rate Experimentation).
- For most propellants, certain levels of local combustion gas velocity (or mass flux) flowing parallel to the burning surface leads to an increased burning rate. This "augmentation" of burn rate is referred to as erosive burning, with the extent varying with propellant type and chamber pressure. The mechanism of increased convective heat transfer to the propellant surface due to turbulence is most likely responsible for this augmentation. For many propellants, a threshold flow velocity exists. Below this flow level, either no augmentation occurs, or a decrease in burn rate is experienced (negative erosive burning). This is illustrated in Figure 5.

Figure 5 -- Erosive burning phenomenon
In Figure 5, propellant "A" exhibits a threshold flow velocity of about 240 ft/sec. Propellant "B" (AP/polyurethane) exhibits a lower threshold velocity with higher chamber pressures. Below this threshold level, an interesting phenomenon occurs -- the burn rate decreases relative to the zero flow level. This is referred to as negative erosive burning, and is possibly the result of changing physical processes of heat transfer that controls the burning rate. At low flow velocity, mass transfer dominates, but as the flow velocity increases, the mechanism of convection becomes increasingly more significant (Figure 5).
Figure 6 -- Heat transfer processes that influence burning rate
An alternative explanation suggests that this effect may be due to partial coverage of the oxidizer (particle) surfaces by the melted binder under the effect of shear stresses in the boundary layer of combustion flow. The KNSB Propellant appears to be particularly susceptible to negative erosive burning.The effects of erosive burning can be minimized by designing the motor with a sufficiently large port-to-throat area ratio (Aport/At). The port area is the cross-section area of the flow channel(s) in a motor. For a hollow-cylindrical grain, this is the cross-section area of the core. As a rule of thumb, the ratio should be a minimum of 2, for a "typical" grain L/D ratio of 6. A greater Aport/At ratio should be used for grains with larger L/D ratios.
To relate the erosive burning rate to the gas flow in the combustion chamber, various empirical laws are used:r = a Pc n [1 + k(G - G*) ] multiplicative law where k is a constant, and G is the specific mass flow rate of the main flow, and G* is a threshold flow rate.
r = a Pc n + k u additive law where k is a constant, and u is the velocity of the main flow.
- In an operating rocket motor, there is a pressure drop along the axis of the combustion chamber, a drop which is physically necessary to accelerate the increasing mass flow of combustion products toward the nozzle. The static pressure is greatest where gas flow is zero, that is, at the front (bulkhead) of the motor. Since burn rate is dependant upon the local pressure, the rate should be greatest at this location. However, this effect is relatively minor and is usually offset by the countereffect of erosive burning.
- Burning rate is enhanced by acceleration of the motor. Whether the acceleration is a result of longitudinal force (e.g. thrust) or spin, burning surfaces that form an angle of about 60-90o with the acceleration vector are prone to increased burn rate. As the majority of the burning surface of most grain configurations is perpendicular to the motor axis, spin (rather than longitudinal acceleration) has a far more profound effect on burning rate. There are three main reasons why spin increases burn rate:
- Rotation reduces the mass flux (flow) at the nozzle throat. This reduction in mass flux has the same effect as a decrease in throat area, thus increased chamber pressure (and consequently higher burning rate) may result.
- Viscous flow patterns are set up in the motor, increasing heat transfer to the propellant surface through greater mass transfer.
- The radial acceleration forces can cause greater retention of the solid phase combustion products near the propellant surface.
For composite motors, a spin induced acceleration of at least 10g's is required before appreciable burn rate augmentation results. Is this a concern for spin-stabilized amateur rockets, then? A simple calculation shows that for a motor with a diameter of 4 inches (10 cm), a spin of 420 RPM is required to develop a 10g acceleration normal to the motor axis. Such a high spin rate is well beyond that required for stabilizing, so for amateur rockets, acceleration augmented burn rate is not a concern.
- Rotation reduces the mass flux (flow) at the nozzle throat. This reduction in mass flux has the same effect as a decrease in throat area, thus increased chamber pressure (and consequently higher burning rate) may result.
Modification of Burning Rate
It is sometimes desirable to modify the burning rate such that it is more suitable to a certain grain configuration. For example, if one wished to design an end burner grain, which has a relatively small burning area, it is necessary to have a fast burning propellant. In other circumstances, a reduced burning rate may be sought after. For example, a motor may have a large L/D ratio to generate sufficiently high thrust, or it may be necessary for a particular design to restrict the diameter of the motor. The web would be consequently thin, resulting in a short burn duration. Reducing the burning rate would be beneficial.There are a number of ways of modifying the burning rate:
- Decrease the oxidizer particle size
- Increase or reduce the percentage of oxidizer (greater O/F ratio)
- Adding a burn rate catalyst or suppressant
- Operate the motor at a lower or higher chamber pressure
- The effect of the oxidizer particle size on burn rate seems to be influenced by the type of oxidizer. Propellants that use AP as the oxidizer have a burn rate that is significantly affected by AP particle size. This most likely results from the decomposition of AP being the rate-determining step (see below) in the combustion process. Propellants that use KN as the oxidizer, however, have a burn rate that is not strongly influenced by the KN particle size. A comparison of burn rate (at ambient pressure) for the KNDX propellant is provided in Figure 7.

Figure 7 -- Effect of oxidizer particle size on burn rate. Click for table.
The "fine" oxidizer grind was obtained by the usual means of milling the "as obtained" potassium nitrate in an electric coffee grinder, for 20-25 seconds per scoopful. The "superfine" grind was obtained by milling the "as obtained" granules in a rock-tumbler, together with several small rocks, for a period of 24 hours. The resulting powder was extremely fine. The increase in average burn rate was about 16%. Bear in mind that this result is valid at ambient pressure (1 atmosphere). Under elevated pressure, the result may well be different, depending on whether the increased burn rate is due to a modified burn rate coefficient, or modified pressure exponent. If the former is modified, then the same effect will occur at elevated pressure. Not so, if the pressure exponent is modified.
Reducing the burn rate by utilizing larger oxidizer particles is not a good means. Characteristic Velocity (c*) measurements of the KNSU propellant were taken with the propellant prepared with as obtained oxidizer granules, and for comparison, with the propellant prepared with "fine" oxidizer particles. The c* measurements were 850 m/s and 911 m/s, respectively. Thus, preparation of the propellant with the larger oxidizer particles resulted in a 7% potential performance loss. Note that the maximum particle size for as obtained granules was about 250 microns. For the "fine" grind, the maximum particles were about 100 microns, and for "superfine", about 20 microns. - The burn rate of most propellants is strongly influenced by the oxidizer/fuel ratio (O/F). A compilation of strand test data conducted at ambient pressure for various O/F ratios for the KNDX and KNSU propellants is given in Figure 8.

Figure 8 -- Burn rate as function of O/F ratio.
Unfortunately, modifying the burn rate by this means is quite restrictive, as the performance of the propellant, as well as mechanical properties, are also greatly affected by the O/F ratio. - Certainly the best and most effective means of increasing the burn rate is the addition of a catalyst to the propellant mixture. A catalyst is a chemical compound that is added in small quantities (typically a few percent or less of the total mass) for the sole purpose of tailoring the burning rate. A catalyst's action is possibly due to a number of means (or combination of means) and probably varies with specific propellant and catalyst type:
- Enhancing fuel decomposition
- Enhancing oxidizer decomposition
- Accelerating vapourized fuel reactions in the gas phase in the combustion zone
- Increasing heat transfer at the propellant surface layer
Some examples of burn rate catalysts are:
- Ferric Oxide (Fe2O3), copper oxide (CuO), Manganese Dioxide (MnO2) are commonly used catalysts in AP based composite propellants, as is copper chromate (Cu2Cr2O5 or 2CuO Cr2O3).
- Potassium dichromate K2Cr2O7 or ammonium dichromate (NH4)2Cr2O7 for AN based mixtures.
- Ferric Oxide (Fe2O3), Iron sulphate (FeSO4) and potassium dichromate for KN-Sugar propellants
- Lampblack (carbon) may slightly increase the burn rate of most propellants through increased heat transfer from the combustion flame to the propellant surface.
The effect of iron compounds on the burning rate of an AP/PBAN propellant is shown in Figure 9.
Figure 9 -- Increase in burn rate from catalyst additives
A recent experiment indicates that ferric oxide may be a particularly effective burn rate catalyst for KNSU. A trial batch of experimental propellant was prepared with 1% ferric oxide (64.4/34.7/1.0 KN/Sucrose/FO), and burn rate measurements of strands taken under ambient conditions. The strands burned vigorously, at an average rate of 6.0 mm/sec. This represents about a 60% increase in burn rate compared to the standard 65/35 KN/Sucrose formulation (see Figure 8). Such a rapid burn rate makes the feasibility of an end-burner grain configuration worthy of investigation.It should be noted that the addition of a burn rate catalyst not only makes a propellant burn more rapidly, but also makes it easier to ignite. This is a double-edged sword, as motor start-up is enhanced, which leads to more efficient use of propellant, and a thrust-time profile more closely matching design curve. However, greater care and precautions must be taken when handling a propellant with a significant amount of catalyst to avoid inadvertent ignition.
A burn rate suppressant is an additive that has the opposite effect to that of a catalyst -- it is used to decrease the burn rate. For AP based propellants, oxamide (NH2 CO2)2 is particularly effective in reducing burn rate, without sacrificing performance. Other potential burn rate suppressants include calcium carbonate, calcium phosphate, ammonium chloride, and ammonium sulphate.
For KNDX, an interesting burn rate suppressant is moisture. If the propellant is prepared with the hydrated fuel, dextrose monohydrate (C6H12O6 . H2O), and minimally heated during casting, the resulting propellant has a moisture content approaching 3.5%. The burn rate (at ambient pressure) is reduced significantly. Experimental measurements showed an average burn rate of 1.42 mm/sec., compared to an average 1.95 mm/sec. for the propellant prepared in the same manner, but with anhydrous dextrose (see Figure 7). This represents a 27% burn rate reduction, with a theoretical performance loss of only about 1%. It is worth noting that the residual moisture has a significant effect upon the mechanical properties of the propellant, producing a "waxy" and rather flexible (albeit viscous, not elastic) grain.
All burn rate suppressants make the grain more difficult to ignite, necessitating an enhanced pyrotechnic or pyrogen ignition system. - For a propellant that follows the Saint Robert's burn rate law, designing a rocket motor to operate at a lower chamber pressure will provide for a lower burning rate (see Figure 2). This effect is more pronounced for a propellant with a higher pressure exponent. If a propellant exhibits plateau or mesa behaviour, this means of obtaining a lower burning rate would be less effective.
Due to the nonlinearity of the pressure-burn rate relationship, it may be necessary to significantly reduce the operating pressure to get the desired burning rate. The obvious drawback is reduced motor performance, as specific impulse similarly decays with reducing chamber pressure.
Combustion Process
Solid propellant combustion is a very complex phenomenon, and understanding and modeling the actual processes involved is difficult. Propellants, in their simplest forms, consist of a dispersion of varying sized oxidizer particles within a matrix of fuel/binder. The combustion process involves a magnitude of subprocesses, or steps. In order to begin to understand the burning rate mechanism it is important to identify the key processes that control the burning. Some of these processes include heating of the solid phase, decomposition of the oxidizer and binder (which burn at different temperatures), possible melting and vapourization, mixing and reactions in the vapour phase, and gas-phase combustion.A number of theoretical models have been proposed to describe the combustion process, including the Beckstead-Derr-Price (BDP) model and the Petite Ensemble Model (PEM). The BDP model proposes that the flame structure of a composite propellant is not homogeneous, but consists of multiple flames and three combustion regions: two kinetics-dominated (reaction) flames and one diffusion flame. The oxidizer breaks down in one reaction flame and sends oxygen into the diffusion flame. Binder decomposition products pre-react in the other reaction flame then rush into the diffusion flame, where they react further with the oxygen. The influential parameters affecting burning rate in these models include the heat of vapourization, the heat conduction into the solid phase, and the flame standoff distances.
One shortcoming of the BDP model is that it considers a single particle size of oxidizer. The PEM model recognizes that most composite propellants contain a wide dispersal of oxidizer particle sizes. Such a scattering is desirable because propellants with a single oxidizer particle diameter are limited to slightly more than an 80% theoretical maximum oxidizer mass fraction. Small oxidizer particles are necessary to fit in between the large ones in order to have a high oxidizer percentage.
The combustion process upon which these models are based is shown in Figure 10.

A key part of the combustion process that determines the burning rate of a propellant is the rate-determining step. As mentioned above, the combustion process is complex and consists of multiple steps. The overall rate at which the burning of a propellant occurs is governed by the slowest step, or rate-determining step. This is usually the decomposition of either the oxidizer or decomposition of the fuel (binder). For ammonium perchlorate (AP) based propellants, it is usually the former. This is why AP particle size plays a big role in burn rate of AP based propellants. For potassium nitrate (KN) based propellants, it would seem to be the latter, or decomposition of the binder that is the rate determining step. This is evidenced by the relatively mild effect of KN particle size on burn rate (Fig. 7). Conversely, a profound difference in burn rate is observed with different binders. KNSU (sucrose binder) burns much more rapidly, in all pressure regimes, than KNSB (sorbitol binder). Epoxy-based potassium nitrate propellants (such as RNX series) burn at a rate far slower than any of the sugar-based propellants.
As it is difficult to theoretically predict a propellant's burn rate with sufficient engineering accuracy, the only recourse is to measure burn rate utilizing any number of proven techniques.
Burn Rate Measurement
There are a number of ways to experimentally determine (or estimate) the burn rate of a particular propellant, and importantly, its relationship to chamber pressure. Three ways will be covered here:- Crawford type Strand Burner apparatus
- Burn rate analysis using the Pressure-Time curve obtained from a motor firing
- Burn rate Ballistic Evaluation Motor
- With the Crawford Strand Burner method of burn rate measurement, a small sample of propellant is burned in a closed firing vessel at a certain constant (or approximately constant) pressure. Each propellant sample, called a strand, is in the form of a thin stick. The strand is electrically ignited at one end, and the time duration for the strand to burn along its length (cigarette fashion) is measured. The strands are usually inhibited along their whole length to ensure that burning only occurs perpendicular to the surface. Various means are used to measure the time duration, such as lead wires embedded in the strand which melt when contacted by the flame front, or by use of thermocouples. The burn rate is obtained by knowing the burning distance as well as the burning time between the lead wires (or thermocouples). Nitrogen is used to pressurize the firing vessel. To effectively characterize the burn rate versus pressure relationship for a particular propellant, 10 or more tests may be performed , at pressures ranging from a few atmospheres, to 100 atmospheres (1500 psi) or more. Complete details of a Strand Burner that I have constructed, and used to characterize the "sugar" propellants, is given in the Strand Burner for Burn Rate Measurements web page.
More recently, I have developed an apparatus that I refer to as a "Delta-P Strand Burner". This is similar to the Crawford strand burner, but is simpler in means of operation. Instead of using thermocouples to sense the time duration that a strand takes to burn a given length, the time duration is measured by monitoring the pressure within the vessel. A strand, of known length, is burned within the pressure vessel, with the pressure being continuously recorded (the pressure rises due to combustion gas generation). The time duration that the strand takes to burn is then taken as the duration over which the pressure changes ("delta P"). This technique has been used with great success in characterizing the Epoxy based propellants.
( View example of Pressure-Time trace) - The instantaneous burning rate of a propellant may be estimated from the pressure-time trace obtained from a motor firing. This method is based on the knowledge that motor chamber pressure and burn rate are directly related in terms of Kn, c* and the propellant density. The burn rate coefficient and the pressure exponent may also be estimated. This method is described in detail in the Burn Rate Determination from a Pressure-time Trace web page.
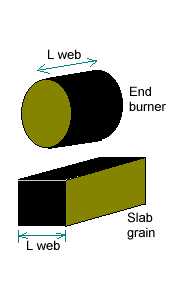
- The third method of determining burning rate of a propellant is by use of a Ballistic Evaluation Motor (BEM). Such a motor is illustrated, in concept, in Figure 11, together with two grain types that may be used in the motor. The principle is simple, with grain ignition occurring on one end (or side, as with the slab grain), and burning along the length of the web. Note that all surfaces are inhibited from burning, except one surface. As the surface area remains constant, the steady-state operating pressure of the motor is constant, and the burning rate is obtained from the web length (L web) divided by the motor burn time.
For a slow burning propellant, the end-burning grain configuration may not be practical (required throat diameter may be too small) to produce the desired pressure. In this case, the slab grain may be the solution, as it allows for a significantly greater burning area.
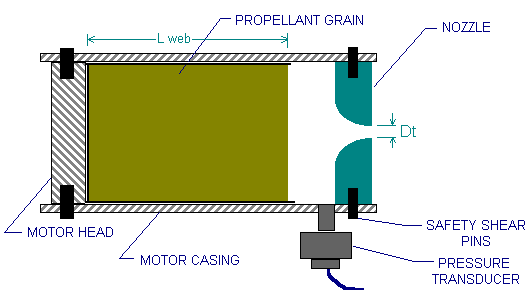
For this method, it is important that the entire burning surface of the grain ignite simultaneously. This may be more ensured by use of an ignition aid coating, such as Combustion Primer, described in the Propellant Igniteability Experiment web page.
One drawback of this method is that several motor firings, as various pressures, each requiring a different throat size (D t), are required to well characterize a propellant.
For more information on erosive burning, an excellent article is the following:
The Solid Rocket Motor- Part 6: Erosive Burning Design Criteria for High Power and Experimental/Amateur Solid Rocket Motors by Charles E. Rogers, Tech Series, High Power Rocketry magazine (Erosive_Burning_Design_Criteria.pdf)
