
Note 1
Potassium Nitrate - Potassium Perchlorate - Sorbitol (KNPSB) propellant
35/30/35 ratio @ 1000 psia chamber pressure
From PROPEP results, for 100 grams mixture:

The effective Molecular Weight is given by dividing the number of GAS moles into the system mass. Since the system mass is 100 grams:
![]()
The mass fraction of condensed phase is given by the total mass of the condensed phase divided by the system mass
The MW of K2CO3 is 138.21 g/mole and the MW of KCl is 74.25 g/mole, thus
Note 2
KNPSB 35/30/35 ratio @ 1000 psia chamber pressure
Mole fractions and mass fractions for each significant combustion product are calculated in the table below:

The table below shows the computation of k, the ratio of specific heats:

The values for Cp and Cs are taken from NIST Chemistry WebBook. Units of Cp and Cs are J/mol-K.
Note that the highlighted range (yellow) is applicable for interpolation of the values at 1858 K, the chamber combustion temperature under consideration.
The Cp for the gas only products and mixture (gas+condensed) is given by

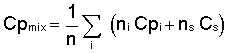
where ni is the number of moles of gas component i , ns the number of moles of condensed component, n the total number of gas moles. The ratio of specific heats for the mixture, for the gas-only, and for two-phase flow is given by
 where
where  = 8.314 J/mol-K (universal gas constant).
= 8.314 J/mol-K (universal gas constant).

where y = X /(1-X).
Note that k for two-phase (gas+condensed) flow is a modified form of the gas-only k'. This is the correct form of k to use in the thermodynamic equations involving products with a significant fraction of condensed-phase particles. The value of k given in the PROPEP output (Cp/Cv) is for the mixture.

with
To = 1858 K
M = 37.17 kg/kmol
k = 1.162 Note: k for the mixture is the proper value to use, as c* represents a static condition
 = 8314 J/kmol-K
= 8314 J/kmol-K
this gives c* = 1004 m/s (3295 ft/s).
The propellant specific impulse is given by the effective exhaust velocity divided by g.
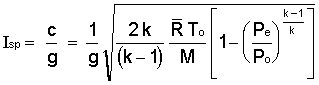
with
To = 1858 K
M = 37.17 kg/kmol
k = 1.095 Note: k for 2-phase flow is the proper value to use, as Isp involves two-phase flow.
Thus, Isp = 174.6 sec.
for standard conditions of Po = 68 atm. (1000 psia) and Pe = 1 atm., and g = 9.806 m/s
(maximum theoretical, assumes frozen equilibrium, and no particle velocity lag or thermal lag).